Below are some of the recent topics Dr. Helenbrook’s lab has been exploring.
“On the Variation of Fricative Airflow Dynamics with Vocal Tract Geometry and Speech Loudness”
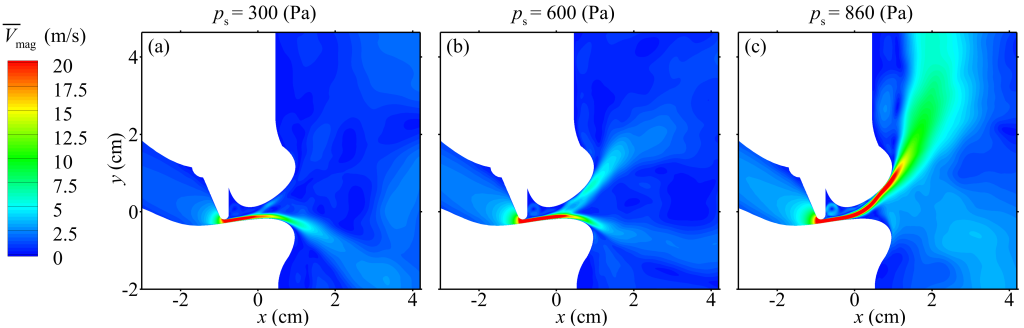
tooth gap height of 1.0 mm at subglottal pressures of (a) 300, (b) 600, and (c) 860 Pa at 0.2 s.
Abstract
Recent studies have determined that the number of respiratory droplets expelled during a short duration of speech can be comparable to that of a cough. Although speaking is typically modeled as a horizontal jet, recent experimental work has shown that there are large angular variations when fricative sounds are produced. To investigate this, two-dimensional vocal tract geometries for a labiodental fricative, [f] and a dental fricative, [θ] were constructed based on magnetic resonance imaging (MRI) during these intonations. Two-dimensional ANSYS-Fluent simulations were performed to investigate the expiratory airflow from the geometries, which showed chaotic unsteady airflow trajectories with maximum velocities ranging from 20 to 40 m/s and jet trajectory angles varying between ±60◦. The simulations highlight the variabilities of the expirated airflow trajectories as a function of the type of utterance, speech loudness, size of the mouth opening, and tongue shape.
“A novel stabilization method for high-order shock fitting with finite element methods”
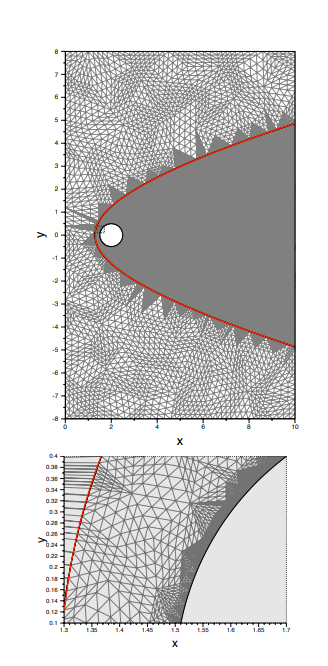
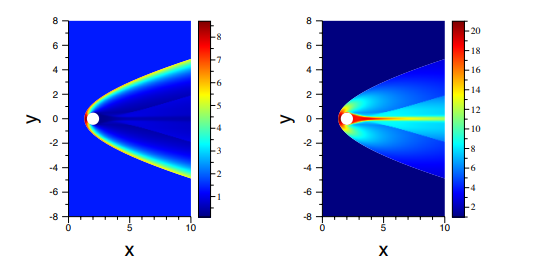
Abstract
A moving-grid, shock-fitting, finite element method has been implemented that can achieve high-order accuracy for flow simulations with shocks. In this approach, element edges in the computational mesh are fitted to the shock front and moved with the shock throughout the simulation. The Euler or Navier-Stokes equations are solved on the moving mesh in an arbitrary Lagrangian-Eulerian framework. The method is implemented in two dimensions in the context of a streamwise upwind Petrov-Galerkin finite element discretization with unstructured triangular meshes and mesh adaptation. It is shown that the shock interface motion equation has a wave nature, and disturbances can propagate along the shock interface. A SUPG stabilization term is introduced to the interface motion equation that is critical for ensuring that interface disturbances do not lead to non-convergent solution behavior. The formal order of accuracy of the scheme is verified, and the performance of the proposed scheme is assessed for both inviscid and viscous problems. It was found that the present scheme predicts smooth and noise-free surface heating for hypersonic flow over a cylinder with purely irregular triangular elements.
“Experimental and Numerical Investigation of the Horizontal Ribbon Growth Process”
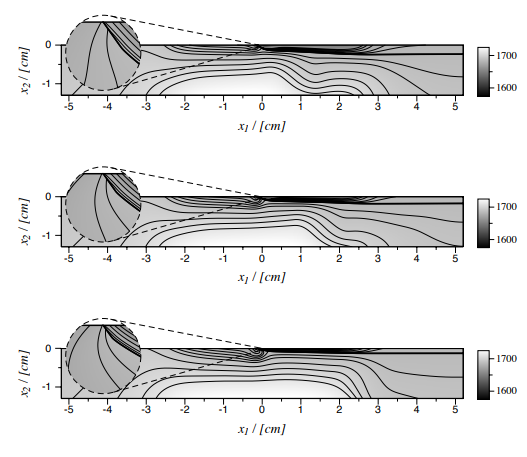
Abstract
Experimental and numerical results are presented on the process of horizontal ribbon growth (HRG) of single-crystal silicon. Experimental data on the leading edge position of the growth front as a function of pull speed is compared to model predictions with and without solidification kinetic effects. Without kinetics, the numerical results predict leading edge positions which are completely different than that observed in the experiment. With kinetics, the leading edge position is predicted typically within 1 mm and the change in position with pull speed also is well predicted. Conclusions from the kinetic model are that the growth occurs through a faceted process where the leading edge is a {111} facet that requires significant supercooling to maintain the growth. An outcome of the model is that the leading edge position versus pull speed response shows a turning point beyond which there are no steady growth solutions. This is consistent with all previously reported experiments on this process, which have reported maximum attainable pull-speeds. These results directly contradict previous conclusions from the “wedge” model of horizontal ribbon growth, which predicts that a large area wedge-shaped growth region exists and that increasing pull speeds simply result in a narrower wedge angle.